二音を同時に鳴らした時にどのような現象が生じるか、 音程に関する諸問題を音楽家の為に科学的に解説したい。
音は空気の振動であり、その振動は波動の性質を持つ。 ただし音は空気以外の媒質中でも伝播する。 例えば水は空気の四倍の伝播度を持つし、 棒状の固体は更に高い伝播度を持つ。 しかし多くの場合、特に音楽に使用される音は、空気を媒体としている。

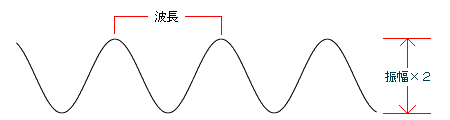
上の図は最も単純な波動の例である。 波の振動の幅を振幅というが、静止状態から振幅だけ上下に振動するので、 波形の山と谷の幅は振幅の二倍になる。 また山から次の山までの距離を波長という。 ある一点に注目して、波が一回振動するのに必要な時間を周期といい、 一秒間に振動する回数を振動数という。周期と振動数の関係は、
周期 = 1 / 振動数
となる。振動数とは一秒間に振動する回数であり、 また一回の振動で一波長分だけ波が進行した事になるのだから、
波の速度 = 振動数 × 波長
で波の速度が求められる。 温度が変化しなければ音波の速度は秒速340メートル程度で一定である。 従って振動数が増えれば波長が短くなる、 のように振動数と波長はほぼ一対一に対応する。
音波の場合、振動数が大きいほど高い音になり、小さいほど低い音に感ずる。 また音の大きさは振幅の大きさで決まり、 音色は振動の波形によって決定する。 人間が聞くことのできる音の振動数は、 おおよそ16ないし50000である。 その中でも実際の音楽に使われる音は、 一秒間に30振動から4000振動ぐらいの範囲となっている。
二つの音の音高差を音程といい、 二つの音がよくとけあう音程を協和音程という。 楽典における協和音程の分類は以下のとおりである。
完全一度はまったく音高同じ、すなわち振動数が等しいことを表す。 完全八度は一オクターブの音程であり、 一方の音の振動数がもう一方の振動数のちょうど二倍である。
一般に音程は振動数の比で表される。 いま振動数の比(振動比)を次の式で定義する。
振動比 = 高い方の振動数 / 低い方の振動数
ただし完全一度のときの振動比は1である。 例えば振動数420の音と振動数280の音の振動比は、 420/280、つまり3/2である。 純正調における協和音程の振動比は次のようになる。
| 音程 | 振動比 |
|---|---|
| 一度 | 1/1 |
| 短三度 | 6/5 |
| 長三度 | 5/4 |
| 四度 | 4/3 |
| 五度 | 3/2 |
| 短六度 | 8/5 |
| 長六度 | 5/3 |
| 八度 | 2/1 |
振動数440よりも一オクターブ高い音の振動数は880であり、 さらに880よりも一オクターブ高い振動数は1760である。 つまり振動数440よりも二オクターブ高い振動数は1760であるので、 二オクターブ差を表す振動比は、
1760 / 440 = 4
である。 振動比の式を変形すれば、
高い方の振動数 = 低い方の振動数 × 振動比
となる。 例えば振動数440と短三度関係を音は(二つ存在するが振動数の大きい方は)、
440 × 6/5 = 528
で求められる。ここで6/5は短三度の振動比である。 更に振動数528と長六度になる音は、長六度の振動比が5/3であるから、
528 × 5/3 = 880
となる。もとの振動数440と、この880の振動比は、
880 / 440 = 2/1
である。一般に二つの音程を加えるには、 二つの振動比の積を求めなければならない。
振動比 = 一方の振動比 × 他方の振動比
例えば短三度と長六度を重ねた音程の振動比は、
6/5 × 5/3 = 2/1
である。この値は先ほどの880/440の値と一致する。
振動数440の純音を鳴らした際、音波は下図のような正弦波を描く。
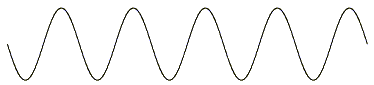
ただ楽音の場合には、この波を基準として、 振動数が整数倍の波が同時に発せられている。 基準となる音を基底音といい、 基底音より振動数が整数倍の音を倍音という。 倍音の含み具合が楽器の音色を決定する大きな一因である。 このように楽音には様々な部分音からなるので、 基底音のことを第一部分音呼び、 そして基底音の二倍の振動数を持つ波を第二部分音と呼ぶ。 振動数440の基底音に対する第二部分音の振動数は880である。 この波は次のような波形を描く。
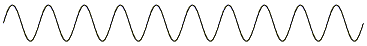
上の二つの波を合成すると、 二つの部分音を持つ音の波形が得られる。
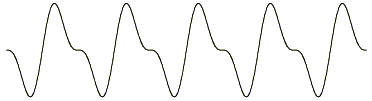
山と山の距離は振動数440の図と同じなので、 我々はこの音を振動数440の高さの音として認識する。 実際の楽器ではこの波形に、振動数三倍の第三部分音、 振動数四倍の第四部分音、 更に振動数の高い部分音が加わり、 楽音の複雑な音色を構成する。
ところで第二部分音と第三部分音の振動比は、
1320 / 880= 3/2
である。振動比(3/2)は五度音程を表す。
このように部分音同士の音程を調べて行くと、 各倍音を音階上に近似できる。 例えば c 音を基底音とすると、 第一部分音から第六部分音まではドイツ音名で次のようになる。
c, c1, g1, c2, e2, g2
譜表上で表すと次のようになる。
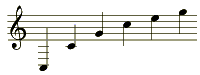
もちろん実際にはより高い倍数の部分音も含まれている。
二音が同時に鳴らされた時に、 滑らかで調和した感じを与える一対の音を、協和二音と定義する。 もちろん完全一度ならば完全に調和する。 次いで調和すると考えられるのが八度音程である。 では八度である c と c1 を例に取り、 この八度の協和度を、第六部分音まで考慮に入れて考えてみよう。 まず c 音の基底音から第六部分音までの部分音列は次のようになる。
c, c1, g1, c2, e2, g2
また c1 音の部分音列は、
c1, c2, g2, c3, e3, g3
である。これら二つの部分音列を対照させると次のようになる。
| c | c1 | g1 | c2 | e2 | g2 |
| c1 | c2 | g2 |
第六部分音までを考えるかぎりでは、 c1音における c3, e3, g3 は c 音と関係しないので省略した。
さてこの部分音列の羅列をみると c1 音の部分音は、 単に c 音の部分音を補っているだけである。 一般的に八度音程であれば、 高い方の音は低い方の音の部分音を補強するだけである。 故にここから不快なうなりは生じるはずもなく、八度は協和二音の代表といえる。
次に c 音と g1 音を考える。これらは十二度音程である。
| c | c1 | g1 | c2 | e2 | g2 |
| g1 | g2 |
これも g1 音の部分音は c 音の部分音を補っているだけであり、 十二度は協和二音といえる。 同様に十五度関係の c 音と c2 音では、
| c | c1 | g1 | c2 | e2 | g2 |
| c2 |
八度音程は振動比2、十二度は振動比3、十五度は振動比4である。 このように一般に振動比が整数のとき、 高い方の音は低い方の音の部分音を補強するだけである。 ところが振動比が整数でなくなると、これとは異なる現象が生じる。 例えば五度の振動比は3/2であり、 五度をなす c 音と g 音の部分音を比較すると次のようになる。
| c | c1 | g1 | c2 | e2 | g2 | ||
| g | g1 | d2 | g2 |
この場合には不協和の性質が含まれていると考えられる。 c2 と d2 の間は一全音(長二度)であるし、 d2 と e2 の間も一全音である。 前者における不快なうなりは、 g 音の第三部分音である d2 と、 c 音の第四部分音である c2 とで生じている。 また後者では第三部分音と第五部分音から生じている。 両者はともに全音の関係であるが、同じ音程であっても、 より基底音に近い c2 と d2 の方が、 より不協和な要素であるといえるだろう。
同じように四度についても考えてみる。
| c | c1 | g1 | c2 | e2 | g2 | ||||
| f | f1 | c2 | f2 | a2 |
第二部分音 f1 と 第三部分音 g1 が一全音を生じる。 また f2 と g2 の間や、 g2 と a2 の間にも一全音がある。 更に e2 と f2 の間は半音(短二度)である。 半音は全音よりも不協和の度合いが強いといえよう。 まとめると四度は五度よりも不協和であると考えられる。
同様にして各音程が生じる全音と半音をまとめたのが次の表である。
| 音程 | 振動比 | 全音をつくる部分音 | 半音をつくる部分音 |
|---|---|---|---|
| 短三度 | 6/5 | 3-4 | 4-5 |
| 長三度 | 5/4 | — | 3-4, 5-6 |
| 四度 | 4/3 | 2-3, 4-6, 5-6 | 4-5 |
| 五度 | 3/2 | 3-4, 3-5 | — |
| 短六度 | 8/5 | — | 2-3, 3-5, 4-6 |
| 長六度 | 5/3 | 2-3, 4-6 | — |
| 八度 | 2/1 | — | — |
表中で部分音の欄に 3-4 と書かれているのは、 それが第三部分音と第四部分音からつくられることを示す。
無論この中では八度が最も協和する協和二音である。 八度を除く音程について、次の指針に従って協和度をはかる。すなわち、
うなりを生じる全音や半音の個数が最も少ないのは、 短三度、長三度、五度、長六度で、これらはそれぞれ二箇所ある。 この中でも半音を生じない五度と長六度がより協和的といえる。 更に序数をみると、五度は 3-4, 3-5 で長六度は 2-3, 4-6 となっており、 長六度の方が五度よりも序数が低いのでより不協和だといえる。 したがって明かに五度がもっとも協和する協和二音といえる。 このような比較から各音程を協和度の高い順に並べると、
完全五度、長六度、短三度、長三度、完全四度、短六度
となる。四度と短六度の比較では、 全音や半音の個数は完全四度の方が多いが、 短六度の場合は三箇所とも全て半音であるので、 これら二つでは短六度の方が不協和であると結論される。 つまり理論上は、驚くべき事に、短六度が最も不協和なのだ、 短三度よりも長三度の方が不協和なのだ。
ただしこれは静的な二つの音程のみを考えているため、 実際の音楽における協和度とは必ずしも一致しない。 たとえば不協和音程でもそれが「解決」されるならば、 その不協和度はそれほどでもなくなる。 しかし五度が最も協和する協和二音であり、 短六度が最も不協和であることに疑いはない。
上で述べた協和二音の協和度の分析は、 あくまで静的な二音に関して述べたものである。 楽曲中では前後の具合や和音の具合によって 同じ音程であっても聞こえ方は変わってくる。 また短六度が長三度の転回であるという意識的な認識によって、 短六度が長三度と同等な協和度を持っていると感じられるようにもなるだろう。 [2001/03/09]
念のために付け加えておくが、 協和度というのは音の濁り具合に対する概念であって、 音楽的な美しさとは必ずしも一致する訳ではない。 辛みや苦みも用い方によっては美味な料理になるように、 不協和も使い方によってまずくもなるし、 新鮮な美しさを生み出す事もできるだろう。 [2001/03/28]
制作/創作田園地帯
2000/02/08初出
無断転載を禁じます。リンクはご自由にどうぞ。
Copyright © 2000-2005 Yoshinori SUDA. All rights reserved.