本書ではエドモン・コステール氏の自然親和性の考え方を簡単に紹介します。
自然親和性を用いた親和性表は、 従来において不可能と思われていたような 複雑な和声をも分析することを可能にします。 自然親和性に付いて説明する前に、 そもそも伝統的な和声学(機能和声)が持つ問題点とは いったい何だったのかを簡単に述べたいと思います。
そもそもの発端は伝統的な和声学では分析不可能な楽曲が登場したことです。 和声としての機能を無視するかのような不協和音の登場、 一方で東洋の音楽などのように和声学では分析できない音楽組織の流入、 そして例外ばかりをかかえるようになった和声学は既にその光を失っていました。
では伝統的な和声学とは一体どのようなものだったのでしょうか。
和声学を支える一つの柱として、倍音共鳴と呼ばれる現象があります。 つまり弦管を問わず多くの楽器が奏でる音というのは、 或音高を鳴らすと同時に その音高の整数倍の周波数を持った音高も同時に鳴っているのです。 これらは自然に発生する音高の重なりですから、 その中に含まれる音程はとても自然な響きを持っています。 代表的には完全八度、完全五度、長三度、短三度などです。 倍音の含み具合が楽器の音色を決める主因になっています。 倍音列は自然に含まれている音程です。
この倍音の音を他の楽器で奏したらどうなるのでしょうか。 たいへん美しいハーモニーになるのです。
そこで和声学では長三和音を基本とする三度累積の和音を 元に分析を出発させました。 そして和音を協和か不協和かという尺度ではかります。 協和とは倍音共鳴の見地からいって澄んでいる和音、 不協和とは反対に濁った和音のことです。 当然ながら不協和よりも協和が優先されます。 というのも不協和和音の後には必ず協和和音を 持ってこなければならないことになっているのです。 これを不協和和音の解決といって 和声学の中でも非常に重要なファクターなのです。
協和 → 不協和 → 協和
和声学のもう一つ重要な考え方に終止形(カデンツ)というのがあります。 まず全ての和音を主和音(T)のグループと、 属和音(D)のグループに分けるのです (さらに下属和音のSというグループもありますが、 ここでは簡単のために割愛します)。 終止形とは楽曲の和声現象をできるだけ圧縮した形であって、 つまり究極的には主和音に始まって、 属和音と主和音を交互に繰り返すというのです。
主和音 → 属和音 → 主和音
こういった終止形の中で主和音は落ちつきを表し、 反対に属和音は主和音に進もうとする緊張感を持ちます。 先ほどの協和・不協和の関係とちょうど対になっていますね。 もちろん不協和和音の解決と終止形の進行は全く別物ですが、 これらがちょうど重なると予想されるように効果的な和声が生まれます。 ここにおいて上の二つをまとめて、
静寂 → 緊張 → 解決
という一つの流れになるのです。 具体的には終止形の属和音の所で、不協和な属七の和音を使用するのです。 この流れは時代とともにエスカレートしていき、 属九の和音、属十一の和音、そして遂に属十三の和音まで登場します。 属十三の和音? 属十三の和音とはドレミファソラシ全ての音で構成されます。 一体どうしてこの和音が「属」和音なのでしょう。 別に主和音の十三の和音と考えてもよさそうです。 それが属十三と分類するのです。 ここに至って終止形という考え方は意味をなさなくなってしまいました。 残ったのは極度に変質化してしまった協和・不協和の軸だけだったのです。
一方で音楽に全く新しい潮流が誕生してきました。 つまり全音階に基づかない楽曲の登場です。 或物は東洋の音階に基づいており、 また或物は全く新しい未知の音階に基づいていました。 或いはセリー(トローペ)と呼ばれる独自の十二音階技法も登場します。 もちろんこれらの音楽にも「和声」という現象そのものは存在するのですが、 その分析において旧来の和声学は全くの無力でした。
こうして音楽理論は混沌とした時代に入ります。 その中で、自然親和性に基づく和声分析を提唱したエドモン・コステール氏は、 混沌とした時代に新たな光を投じたといっても過言ではないでしょう。
(補足)調性を破壊した要因としては、 例えば無制限な半音階法であったり、複調による主調の欠如であったり、 二次属和音や解決しない不協和音など、数え上げれば無数にあります。 いずれにしても不協和というのがポイントとなる事に疑いはありません。 [2001/03/28]
自然親和性とは二つの音高の関連性の深さの事です。 例えば同じ音高、すなわち完全一度は自然親和性を持っているといいます。 エドモン・コステール氏は自然親和性を有している音程として、 完全八度(完全一度)、完全五度(完全四度)、 および連続移高の半音、を挙げています。 連続移高とは旋律的に非常に滑らかな動きをする音程を指し、 通常の十二平均律では半音になります。
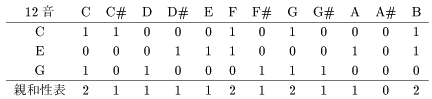
さて自然親和性による和音の分析では、 親和性表を書いてみると見通しがよくなります。 ためしに長三和音 {C, E, G} の親和性表を書いてみましょう。

最上段には十二音が書かれています。 二段目の C の行を見て下さい。 ここには C と自然親和性を持っている音に1、そうでない場合には0を書いています。 例えば C# は半音関係なので1、F は四度関係で1としているのです。 同様に E と G の行も完成させます。 最後に表を縦に見て各列の和をとっていきます。 これが最下段の親和性表になるのです。 親和性表は {C, E, G} の和音が十二音の各音に どれだけ自然親和性を持っているかを表しています。 例えば C# には 1 が入っているので、 この和音の一カ所から親和性を持っているのです。 反対に A# には 0 となっています。 つまり A# という音はこの和音とは何らの親和性も持っていないということです。
さて上の親和性表の C, E, G の所を見て下さい。 それぞれ 2, 1, 2 となっていますね。 これらの数字は和音 {C, E, G} がその構成音に対する自然親和性を表している訳です。 そこでこの数を足し合わせた 5 は、 {C, E, G} が C, E, G の各音に対して どれだけ親和性を持っているかを表したものです。 このように親和性表の数を足し合わせた数を牽引可能性といいます。 言い換えると牽引可能性が高い程、その和音との関連が強いということです。
では {C, E, G} に対する C, E, G の牽引可能性である 5 は、 そもそも何を示しているといえるのでしょう。 結論をいうと、これは和音 {C, E, G} 自身の安定度を示しているいるのです。 この和音は 5 という度合いで自分自身を支えているのです。
それでは牽引可能性 5 というのは安定な方なのでしょうか、 不安定な方なのでしょうか。 これは簡単な方法で測定することができます。 もう一度親和性表を見て下さい。 そもそも或音が持っている親和性は全部で五カ所です。 ここでは三和音の親和性表を書いているのですから、 最下段の合計は 15 になっているはずです。 つまり十二音の各音に対しては平均で 15/12 の数になっているのです。 ここから三音の合計を求めるのですから、15/12 の三倍の 15/4、 つまり 3.75 が牽引可能性の平均値になります。 牽引可能性 5 は平均値を大きく上回っていますから、 長三和音 {C, E, G} は安定した和音といえるのです。 このような和音は特有安定性を持っているといいます。
自然親和性の考えたかを用いて全音階の和声を分析してみましょう。 話を簡単にするために全音階の中でもハ長調を取り上げ、 また従来の和声学と対照させた形で議論を進めていきます。 (余談: そもそもハ長調もト長調も、十二の全ての長調は同じ音階に基づいています。 現在のような十二等分平均律で調律した楽器を使用する限り、 各調の間に有意な差を認めることはできません。 ただしピアノは黒鍵と白鍵では発音構造が異なり、その音色が異なります。 よって黒鍵を多用するほど大人びた落ちついた雰囲気、 ハ長調のように白鍵だけを使用するとハキハキとした軽快な雰囲気になるのです。 注意して欲しいのはピアノに調性の顔があっても これが調性による差ではなく白鍵と黒鍵の音色の違いによるものだということです。)
もう一度 {C, E, G} の親和性表を見てみましょう。

これは特有安定性を持った和音でした。 よって主和音 I は安定的であるといえます。
次に主和音 I から下属和音 IV へと連結することを考えてみましょう。 下属和音とは {C, F, A} によって構成される和音です。 上の親和性表の C, F, A はそれぞれ 2, 2, 1 となっており、 合計すると 5 になっています。 つまり {C, E, G} の {C, F, A} への牽引可能性が 5 ということです。 先ほども述べたように、この場合の牽引可能性の平均値は 3.75 でした。 つまり 5 というのは平均値を上回っており、{C, E, G} から {C, F, A} への進行は 「自然」に行うことができるのです。 これは I - IV という進行の裏付けでもあります。
同様に属和音 V への進行においても、その牽引可能性は 5 となっています。
主和音 I から属七 V7 への連結はどうでしょうか。 属七の構成音は {D, F, G, B} ですから、それぞれ 1, 2, 2, 2 です。 よって牽引可能性は 7 となります。 四音を選んだ場合の牽引可能性の平均値は 5 ですので、I - V7 という 進行は、平均以上の牽引可能性を持っていることが分かります。
次に下属和音 IV から属和音 V への連結を考えてみましょう。 まず下属和音 {C, F, A} の親和性表は次のようになります。
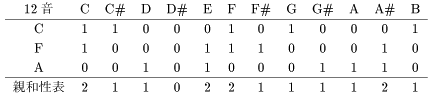
もちろん下属和音は主和音と同じ長三和音ですから特有安定性を持っています。 属和音 {D, G, B} の牽引可能性は 3 です。 これは平均 3.75 を下回っています。 ところが属七 {D, F, G, B} は牽引可能性 5 で、平均の 5 の水準まで上がります。 下属和音 IV からの進行では属和音 V よりも属七 V7 の方が 優位であると結論出来ます。
同様に全ての和音連結における牽引可能性を求められますがここでは省略します。 また同様に短調の和音進行も分析できるでしょう。
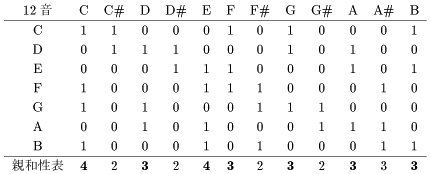
さて次に全く異なるアプローチでハ長調を分析します。 つまりハ長調の構成音 {C, D, E, F, G, A, B} の親和性表を調べるのです。
音階を和音のように分析する事に疑問を持つかも知れません。 しかし和音と旋律、あるいは和音と音階というのは表裏一体となるものです。 その代表的なものに分散和音(アルペジオ)と呼ばれる奏法があります。 分散和音は旋律でありながら和音という名前が付けられているのであって、 つまり和音と旋律というのは言葉で書く以上に境界の曖昧なものなのです。 和音というのは単にどこからどこまでをひとまとまりにするか、 のスケールの問題に帰着します。 例えばハ長調で書かれた曲というのは、 ハ長調という和音の分散和音と見なすことができますし、 また転調という現象は、 例えばハ長調という和音からト長調という和音への 「和音連結」と見ることも可能です。
ハ長調の親和性表に話を戻しましょう。 この和音 {C, D, E, F, G, A, B} は特有安定性をもっていることが分かります。 また C と E という音に強い親和性を持っているのも特徴的です。 主和音 {C, E, G} の牽引可能性の高さも目に付きます。 六度の和音の {C, E, A} は主和音と同じだけの牽引可能性を持っています。 その他、この親和性表は我々に多くのことを物語ってくれるでしょう。
自然親和性の利点は何といってもその適用範囲の広さに尽きます。 長三和音など存在しない五音音階であっても、 あるいはそもそも十二等分平均律に基づかない音階であっても、 例えば二十四等分平均律さえも分析することができるのです。 和音という軸から再び楽曲を包括的に説明することが可能になるのです。
しかし一方で疑問点がないこともありません。 どうして八度と五度と半音だけが自然親和性なるものを持っているのでしょうか。 特に半音において疑問となるのですが、 同時的な和音と旋律的な和音を一様に分析することができるのでしょうか。 同じ半音関係を同時に響かしても、 直近の半音とオクターブ違いの半音では明らかに耳に与える印象が異なります。 こういった点はいかに扱えば良いのでしょうか。 その他、まだまだ改善の余地の多い理論でありますが、 にもかかわらず自然親和性が有益な情報を与えてくれることに疑いはありません。
和声よ、永遠なれ。 音楽よ、永遠なれ。
自然親和性については、 エドモン・コステール著、小宮徳文訳の 『和声の変貌 - 音高組織の論理』(音楽之友社刊、1980年) に拠ります。より詳細な議論はこの本を読んで頂きたいと思います。
制作/創作田園地帯
2001/01/26初出
無断転載を禁じます。リンクはご自由にどうぞ。
Copyright © 2001-2005 Yoshinori SUDA. All rights reserved.