リーマンの短調

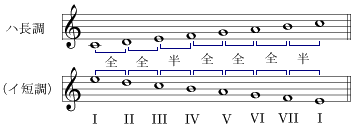
長調と短調を総じて全音階と称し、調性組織における最も根幹をなす。調性組織においては、長調と短調が互いに相反する性質を持つべきとして、時に意識的に、時に無意識的に、或いは楽式的な構造として、二つの音階を対照的な調として捉えられている。長調を本来の姿とすれば、短調は鏡に写った虚像である。

同主調は、同名調ともいうが、ハ長調とハ短調のように、主音を同じくする長調と短調を指す言葉である。同主調の長調と短調は調号で三つ分だけ離れている訳であるから、二つの調は構成音から見ればそれほど近いともいえない。しかしならが主音が同一であるというのは近親関係を感じさせるに充分である。特に和声学では理論の上で同等に扱われており、例えばハ短調におけるカデンツは、調号と臨時記号を全て取り外せばハ長調のカデンツとなるのである。

平行調は、イ短調とハ長調のように、調号の同じ二つの長調と短調を指す。調号が同じという事は、主音や主和音の用い方や導音の向かう先によってのみ、二つの調を区別できるのであって、両者は非常に近い関係にあるといえるだろう。理論的には転調や一時的な借用が簡便に行われ、時として単なる代理和音として他調である事さえ意識されない。しかし一方で短調に対する平行長調は、ちょうど長調と属調の関係のように考えられることがあり、例えばソナタ形式において短調の第一主題に対して平行長調の第二主題を用いる等である。

同主調も平行調も、長調と短調が理論的に同等とする考えの表れであるが、いずれも両調を平行移動的な構造として捉えている。長調の五度上の三和音を属和音と呼べば、短調の五度上の三和音も属和音なのである。

一方でフーゴ・リーマンは長調と短調に対する独自の理論を展開した。下倍音という仮想的な現象によって説明される彼の理論は、非常に理にかなっているよで、また幾何学的な美しさを持った理論である。この理論によるとハ長調と対をなす短調は次のようになる。

リーマンの短調（譜例）

長調と短調が上下転回したシンメトリーを成す点に注目して欲しい。上記の短調ではホの音で音階が開始し、そしてホの音で終結する。音階的に見れば全音と半音の関係が完璧に保存されている。

この短調における主和音はもちろんイ・ロ・ホであって、しかし基本位置における根音はホであってイではない。旋律も和音も長調を上下反対に線対称に見た形になる。つまり長調では根音上に長三度上と更にその短三度上の音を重ねる訳だが、この短調は根音ホの長三度下と更に短三度下の音を重ねているのである。また下降音階に対して和音記号を付している点も見逃せない。すなわち通常の短調ではイ・ヘ・ニの和音は下属和音となるが、リーマンの短調ではイを根音とする属和音である。従ってこれに三度下の音を加えたイ・ヘ・ニ・ロの和音は属七として取扱い、上下反転させた長調の属七のように解決する。

さて実際にこの方法で短調を奏して見れば、予想以上にカデンツを持った和声を奏でる事が出来るのである。例えば I - VI - IV - V₇ - I といった和声も、そのニュアンスを残したまま、短調上に再現される。

和声進行の譜例

そもそもこの短音階は下倍音という仮定に基づき、つまり楽音というのは或音高に対してそれより高い音を含んでいてこれが倍音であるが、これを基本となる音の低い方向にも拡張したものが下倍音である。通常の倍音は基底音に対して八度上、五度上、四度上、長三度上、短三度上などと続くのに対して、或音の下倍音は基底音の八度下、五度下、四度下、長三度下、短三度下のようになる。

このような下倍音は通常の楽音には実在しないのであるから、リーマンの全くの仮想であるといえるが、理論的な整然さは格別のものがある。また近年の電子楽器の発展によって下倍音が全くの仮想ともいえなくもなくなっている。例えばシェパードの無限音階における音は、上倍音と下倍音を同時に持っていると考えられなくもない。

結尾

視点が変われば新たなインスピレーションが湧いてくる。どうして音楽ってこんなにも楽しいのだろう。